Merkle Trees

Feel free to skip this section if you are well versed with Merkle trees.

What is a merkle tree?

Merkle trees are a data structure with the key benefit of being efficient (but not efficient enough for Ethereum's scaling ambitions) to prove that a certain piece of data exists in the Merkle tree. They enable efficient verification of the contents of a large dataset (i.e. transactions, files).

Creating a Merkle tree

Let's break down the following diagram of a Merkle tree.

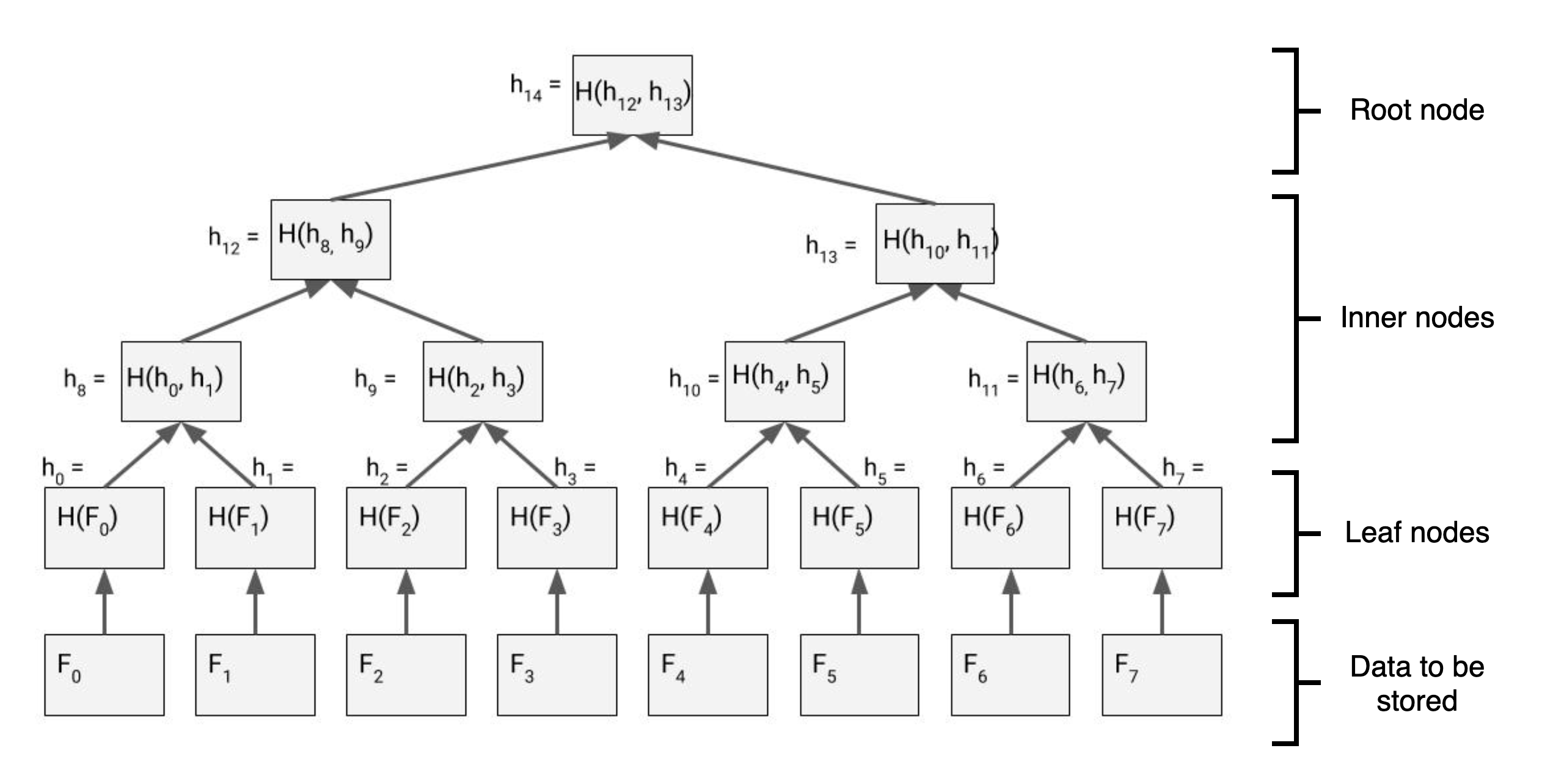
Figure 1. A Binary Merkle Tree¹

We start from the bottom. Let's suppose we have 8 data elements ($F_0, F_1, ..., F_7$) that we want to store in the Merkle tree. These data elements could be anything - blockchain transactions, files, numbers or strings, etc. We convert each individual data element into a leaf node using a cryptographic hash function. $H(F_0)$ is the output of the cryptographic hash function applied to $F_0$, or the hash of $F_0$

The important properties of a cryptographic hash function for a Merkle tree are:

1. Mapping arbitrary-sized data to a fixed-size hash (or digest). So regardless of our input data being a few bytes or multiple megabytes, we will get the same-sized hash.

2. Collision resistance, meaning that it is infeasible for two distinct inputs to have the same output hash, and changing even one bit in the input data will result in a completely different output hash.

Keccak256 is the cryptographic hash function of choice for the Ethereum protocol, and it outputs a fixed-size hash of 32 bytes or 256 bits.

To create the first or bottommost layer of inner nodes, we take two adjacent leaf nodes and apply the cryptographic hash function again to the pair. So in the diagram, the leaf nodes $h_0=H(F_0)$ and $h_1=H(F_1)$ are concatenated to provide the input to the hash function, and the output $H(h_0, h_1)$ becomes the inner node $h_8$ that is the parent to these two leaf nodes. We repeat this process for every pair of leaf nodes, hashing 8 leaf nodes into 4 inner nodes.

To create the next layer of inner nodes, we repeat this process with the layer of inner nodes we just generated. With each layer we halve the number of inner nodes. Eventually after successive rounds of hashing, we reach a layer with only 1 node. We stop here and call this single node the merkle root. The merkle root is a 32-byte string (in the case of Keccak256) which commits all the original data elements.

Verifying data with the Merkle root

1. Verifying whether any leaf node was tampered with

Due to the collision-resistance property of the hash function, any change in any of the original data elements will result in a different merkle root. So if for example we have a Merkle tree of transactions, tampering with any single transaction record would result in a different Merkle root. So by reconstructing the Merkle tree for a given transaction set and checking the root - a single 32-byte string - we are able to check whether a transaction set of any size was tampered with.

2. Verifying that a leaf node exists in a Merkle tree

Continuing with our example of a Merkle tree of transactions, suppose we are given a transaction $T$ that we are told is the same as $F_3$ in the original set of transactions ($F_0, F_1, ..., F_7$). We want to verify that:

i.) $T$ is identical to $F_3$

ii.) $T$ is in the original set of transactions.

We can achieve this with a Merkle proof.

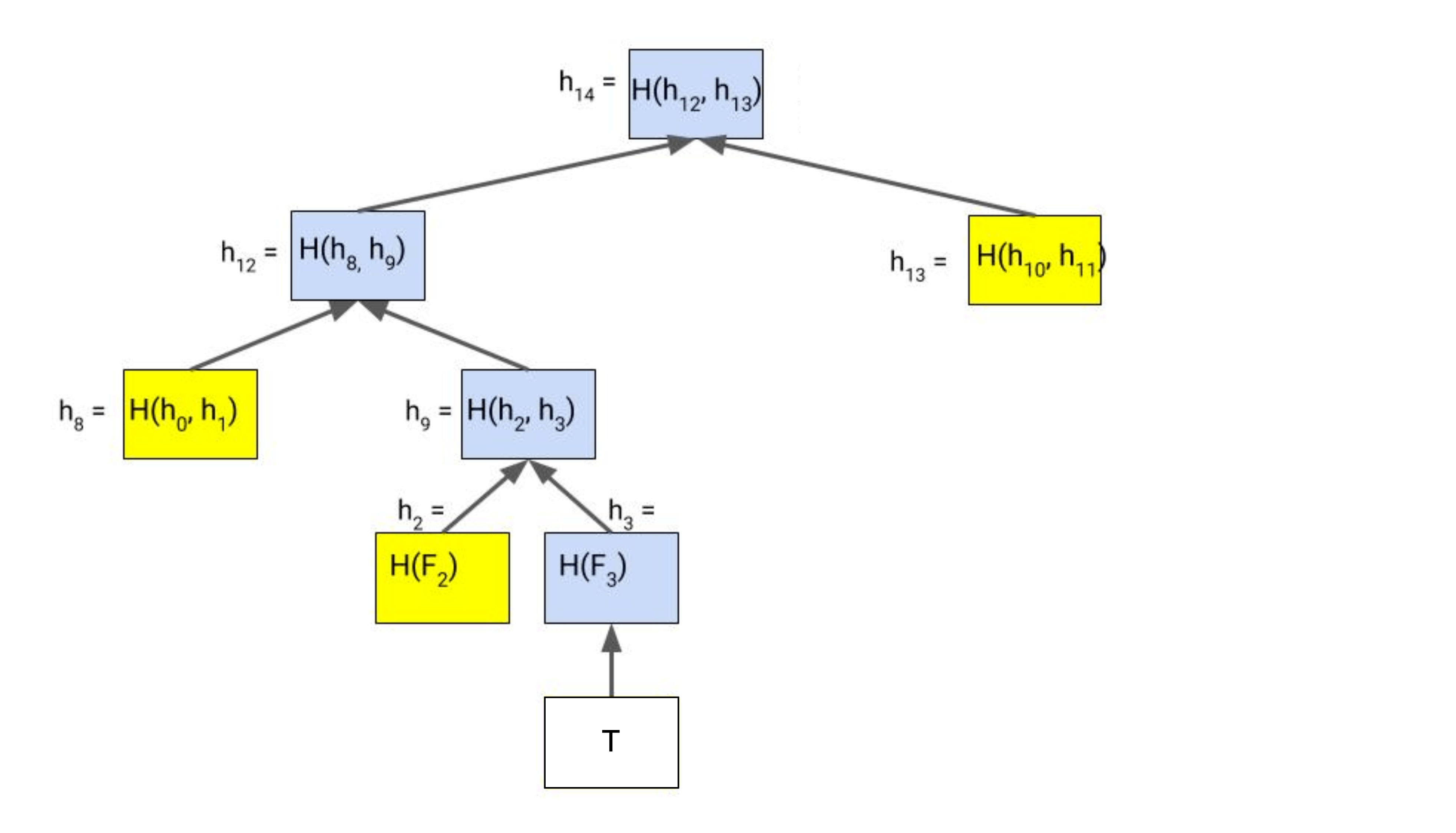
Figure 2. The Merkle proof (in yellow)²

The Merkle proof contains all of the sister nodes which are required to reconstruct the Merkle root. In our diagram our Merkle proof will be $[h_2, h_8, h_{13}]$.

Visually we are walking the path from the leaf node we are attempting to prove, to the root node. So been given the position (within the original transaction set) and supposed contents of $F_3$, and the Merkle proof, our steps to reconstruct the Merkle root would be:

1. Get $h_3 = H(T)$
2. Get $h_9 = H(h_2, h_3)$
3. Get $h_{12} = H(h_8, h_9)$
4. Get Merkle root $= h_{14} = H(h_{12}, h_{13})$

We can then check if Merkle root we got from this process, is the same as the original Merkle root that was committed. If it is identical, then we have proved that $T$ is $F_3$ in original transaction set.

Notice that for a binary Merkle tree, since the Merkle proof requires one node for each level, the space complexity of the Merkle proof is $O(\log_2 n)$. If we stored a million leaf nodes in the Merkle tree, our Merkle proofs would require $\log_2 1,000,000 \approxeq 20$ nodes.

k-ary Merkle Trees

So far we have only considered binary Merkle trees where each inner node has two children (a branching factor of 2). It is also possible to change the branching factor to an integer $k$, such that each inner node has $k$ children, and is the hash of all $k$ children. This has the effect of reducing the height of the Merkle tree.

Unfortunately this also increases the Merkle proof size to $O(k \log_k n)$.

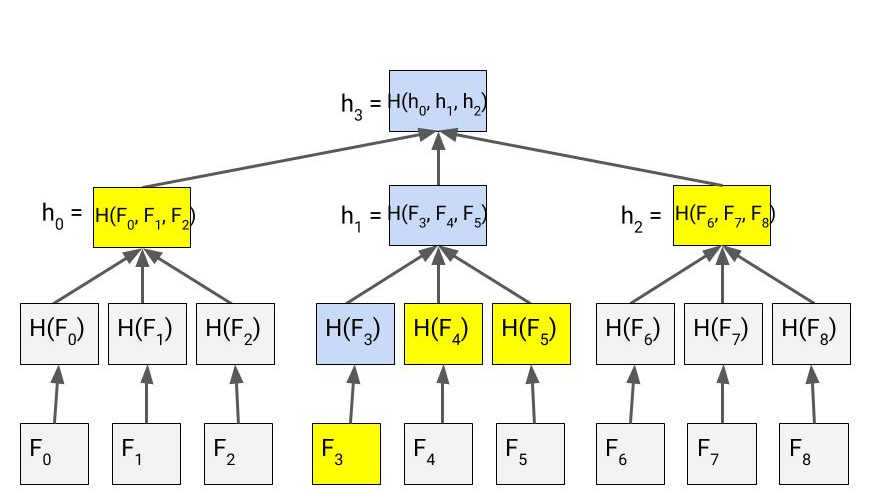
Figure 3. Merkle proof for a 3-ary Merkle Tree (in yellow)³

For each level, the Merkle proof now requires $k-1$ sister nodes for each level in the Merkle tree. This increases the proof size, despite the reduction in the number of Merkle tree levels (i.e. the height).

$$\frac{k-ary\:Merkle\:proof\:size}{Binary\:Merkle\:proof\:size} = \frac{(k-1) \log_k n}{\log_2 n}=\frac{(k-1) \frac{\log_2 n}{\log_2 k}}{\log_2 n}=\frac{k-1}{\log_2 k} > 1\;for\;any\;k > 2$$

If we stored a million leaf nodes in a 3-ary Merkle tree, our Merkle proofs would require $3 \log_3 1,000,000 \approxeq 38$ nodes.

1, 2, 3. Images modified from Kuszmaul's paper